PENALARAN
NAMA
: Dewi Laras
Wijayanti
NPM
: 12114876
KELAS
: 3KA10
MATA KULIAH
: Peng.Teknologi Sistem Cerdas
10.1
Ketidakpastian
Kecerdasan
buatan dikembangkan untuk membuat agar mesin (komputer) dapat melakukan
pekerjaan seperti dan sebaik manusia. Sistem Pakar merupakan bagian dari
kecerdasan buatan yang mengandung pengetahuan dan pengalaman yang dimasukkan
oleh satu atau banyak pakar ke dalam satu area pengetahuan tertentu.
Pengetahuan dan pengalaman yang ada dalam dunia nyata yang akan
direpresentasikan kedalam sistem pakar penuh dengan unsur ketidakpastian dan
kesamaran.
Beberapa
metode yang sering digunakan untuk menangani masalah ketidakpastian dan
kesamaran adalah dengan menggunakan teknik probabilitas, faktor kepastian dan
logika fuzzy. Teorema Bayes merupakan bagian dari teknik probabilitas yang
menekankan pada konsep probabilitas hipotesis dan evidence, sedangkan teknik probabilitas
dengan teori Dempster-Shaffer menekankan pada konsep beliefe dan plausability.
Pada metode dengan faktor kepastian menekankan pada nilai kepercayaan yang
diberikan oleh seorang pengguna dan pakar.
Pada metode dengan logika fuzzy menekankan
pada derajat keanggotaan dari suatu evidence pada suatu himpunan fuzzy sehingga
mampu menangani masalah kesamaran. Untuk memberikan solusi yang lebih baik,
metode-metode yang ada bisa dikombinasikan antara yang satu dengan yang lainnya
10.2
Probabilitas dan teorema Bayes
Teorema
Bayes dikembangkan dengan berbagai ilmu termasuk untuk penyelesaian masalah
sistem pakar dengan menetukan nilai probabilitas dari hipotesa pakar dan nilai
evidence yang didapatkan fakta yang didapat dari objek yang diagnosa. Teorama
Bayes ini membutuhkan biaya komputasi yang mahal karena kebutuhan untuk
menghitung nilai probabilitas untuk tiap nilai dari perkalian kartesius.
penerapan Teorema Bayes untuk mencari penerapan dinamakan inferens Bayes.
Contoh
Soal :
Sebuah perkantoran biasanya membutuhkan tenaga listrik yang cukup agar semua aktifitas pekerjaannya terjamin dari adanya pemutusan aliran listrik. Terdapat dua sumber listrik yang digunakan PLN dan Generator. Bila listrik PLN padam maka secara otomatis generator akan menyala dan memberikan aliran listrik untuk seluruh perkantoran. Masalah yang selama ini mengganggu adalah ketidak satabilan arus (voltage) Listrik. Selama beberapa tahun terakhir, diketahui bahwa perkantoran itu menggunakan listrik PLN adalah 0.9 dan peluang menggunakan generator adalah 0.1 peluang terjadi ketidak stabilan pada arus PLN maupun generator masing-masing 0.2 dan 0.3.
Permasalahan ini di ilustrasikan Sebagai berikut :
E : Peristiwa listrik PLN digunakan
Ec : Peristiwa listrik Generator digunakan
A :Peristiwa terjadinya ketidak stabilan arus
Peristiwa A dapat ditulis sebagai gabungan dua kejadian yang lepas
Sebuah perkantoran biasanya membutuhkan tenaga listrik yang cukup agar semua aktifitas pekerjaannya terjamin dari adanya pemutusan aliran listrik. Terdapat dua sumber listrik yang digunakan PLN dan Generator. Bila listrik PLN padam maka secara otomatis generator akan menyala dan memberikan aliran listrik untuk seluruh perkantoran. Masalah yang selama ini mengganggu adalah ketidak satabilan arus (voltage) Listrik. Selama beberapa tahun terakhir, diketahui bahwa perkantoran itu menggunakan listrik PLN adalah 0.9 dan peluang menggunakan generator adalah 0.1 peluang terjadi ketidak stabilan pada arus PLN maupun generator masing-masing 0.2 dan 0.3.
Permasalahan ini di ilustrasikan Sebagai berikut :
E : Peristiwa listrik PLN digunakan
Ec : Peristiwa listrik Generator digunakan
A :Peristiwa terjadinya ketidak stabilan arus
Peristiwa A dapat ditulis sebagai gabungan dua kejadian yang lepas
Dengan menggunakan
probabilitas bersyarat maka :
Diketahui:
P(E)=0.9 P(E’)=0.1
P(A|E)=0.2 P(A|E’)=0/3
Sehingga:
P(A)=P(E).P(A|E)+P(E’).P(A|E’)
=(0.9).(0.2)+(0.2).(0.3)
=0.21
Kembali pada permasalahan diatas, bila suatu saat diketahui terjadi ketidak stabilan arus listrik, maka berapakah probabilitas saat itu aliran listrik berasal dari generator ? Dengan menggunakan rumus probabilitas bersyarat diperoleh.
P(E’|A)=P(E’∩A)/P(A)
=P(E’).P(A|E’)/P(A)
=0.03/0.21=0/143
Peristiwa B1,B2,….,Bk merupakan suatu sekatan(partisi) dari ruang sampel S dengan P(Bi)≠0 untuk i=1,2,…,k maka setiap peristiwa A anggota S berlaku:
P(E)=0.9 P(E’)=0.1
P(A|E)=0.2 P(A|E’)=0/3
Sehingga:
P(A)=P(E).P(A|E)+P(E’).P(A|E’)
=(0.9).(0.2)+(0.2).(0.3)
=0.21
Kembali pada permasalahan diatas, bila suatu saat diketahui terjadi ketidak stabilan arus listrik, maka berapakah probabilitas saat itu aliran listrik berasal dari generator ? Dengan menggunakan rumus probabilitas bersyarat diperoleh.
P(E’|A)=P(E’∩A)/P(A)
=P(E’).P(A|E’)/P(A)
=0.03/0.21=0/143
Peristiwa B1,B2,….,Bk merupakan suatu sekatan(partisi) dari ruang sampel S dengan P(Bi)≠0 untuk i=1,2,…,k maka setiap peristiwa A anggota S berlaku:
Digunakan bila ingin
diketahui probabilitas P(B1|A),P(B2|A)….,P(Bk|A) dengan rumus sebagai berikut :
Suatu generator
telekomunikasi nirkabel mempunyai 3 pilihan tempat untuk membangun pemancar
sinyal yaitu didaerah tengah kota, daerah kaki bukit dan daerah tepi pantai,
dengan masing-masing mempunyai peluang 0.2,0.3 dan 0.5. Bila pemancar dibangun
ditengah kota, peluang terjadi gangguan sinyal adalah 0.05. Bila pemancar
dibangun dikaki bukit, peluang terjadinya gangguan sinyal adalah 0.06. Bila
pemancar dibangun ditepi pantai, peluang gangguan sinyal adalah 0.08.
A. Berapakah peluang terjadinya gangguan sinyal ?
B. Bila diketahui telah terjadinya gangguan pada sinyal, berapa peluang bahwa operator tersebut ternyata telah membangun pemancar di tepi pantai ?
Misal :
A = Terjadi ganguan sinyal
B1 = Pemancar dibangun di tengah kota
B2 = ----------------------------di kaki bukit
B3 = ----------------------------di tepi pantai
Maka :
A. Peluang terjadinya ganguan sinyal
P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)
= (0,2).(0.05)+(0.3)(0.06)+(0.5)(0.08)=0.001+0.018+0.04=0.068
A. Berapakah peluang terjadinya gangguan sinyal ?
B. Bila diketahui telah terjadinya gangguan pada sinyal, berapa peluang bahwa operator tersebut ternyata telah membangun pemancar di tepi pantai ?
Misal :
A = Terjadi ganguan sinyal
B1 = Pemancar dibangun di tengah kota
B2 = ----------------------------di kaki bukit
B3 = ----------------------------di tepi pantai
Maka :
A. Peluang terjadinya ganguan sinyal
P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)
= (0,2).(0.05)+(0.3)(0.06)+(0.5)(0.08)=0.001+0.018+0.04=0.068
10.3 Faktor Kepastian (
Certainty Factor)
Faktor kepastian
merupakan cara dari penggabungan kepercayaan (belief) dan ketidapercayaan (unbelief)
dalam bilangan yang tunggal. Dalam certainty theory, data-data
kualitatif direpresentasikan sebagai derajat keyakinan (degree of belief).
Tahapan Representasi
Data Kualitatif
Tahapan dalam
merepresentasikan data-data kualitatif :
kemampuan untuk
mengekspresikan derajat keyakinan sesuai dengan metode yang sudah dibahas
sebelumnya.
kemampuan untuk
menempatkan dan mengkombinasikan derajat keyakinan tersebut dalam sistem
pakar.
Dalam mengekspresikan
derajat keyakinan digunakan suatu nilai yang disebut certainy factor (CF) untuk
mengasumsikan derajat keyakinan seorang pakar terhadap suatu data.
Formulasi Certainy
Factor
Dimana :
CF = Certainy Factor (faktor
kepastian) dalam hipotesis H yang dipengaruhi oleh fakta E.
MB=Measure of Belief (tingkat
keyakinan), adalah ukuran kenaikan dari kepercayaan hipotesis H dipengaruhi
oleh fakta E.
MD=Measure of Disbelief (tingkat
ketidakyakinan), adalah kenaikan dari ketidakpercayaan hipotesis H dipengaruhi
fakta E.
E = Evidence (peristiwa
atau fakta).
H = Hipotesis (Dugaan).
10.4 Teori
Dempster-Shafer
Dempster-Shafer
Teori Dempster-Shafer adalah
suatu teori matematika untuk pembuktian berdasarkan belief
functions and plausible reasoning (fungsi kepercayaan dan
pemikiran yang masuk akal), yang digunakan untuk mengkombinasikan potongan
informasi yang terpisah (bukti) untuk mengkalkulasi kemungkinan dari suatu
peristiwa. Teori ini dikembangkan oleh Arthur P. Dempster dan Glenn Shafer.
Secara umum Teori Dempster-Shafer ditulis
dalam suatu interval:
[Belief,Plausibility]
Belief
Belief (Bel)
adalah ukuran kekuatan evidence (gejala) dalam mendukung suatu
himpunan bagian. Jika bernilai 0 maka mengindikasikan bahwa tidak ada evidence,
dan jika bernilai 1 menunjukan adanya kepastian.
Plausibility
Plausibility (Pl)
dinotasikan sebagai:
Pl(s)= 1 – Bel(¬s)
Plausibility juga
bernilai 0 sampai 1. Jika kita yakin akan –s, maka dapat dikatakan bahwa Bel(¬s)=1,
dan Pl(¬s)=0. Plausability akan mengurangi tingkat kepercayaan
dari evidence. Pada teori Dempster-Shafer kita mengenal adanya frame
of discernment yang dinotasikan dengan θ dan mass function yang
dinotasikan dengan m. Frame ini merupakan semesta
pembicaraan dari sekumpulan hipotesis sehingga disebut dengan environtment.
Misalkan: θ = {A, B, C,
D, E, F, G, H, I, J}
Dengan :
A = Gagal Ginjal Kronik
B = Kanker Ginjal
C = Pielonefritis
D = Sindroma Nefrotik
E = Hidronefrosis
F = Kanker Kandung Kemih
G = Ginjal Polikista
H = Nefritis Tubulointerstisialis
I = Sistitis
J = Infeksi Saluran Kemih
Dengan :
A = Gagal Ginjal Kronik
B = Kanker Ginjal
C = Pielonefritis
D = Sindroma Nefrotik
E = Hidronefrosis
F = Kanker Kandung Kemih
G = Ginjal Polikista
H = Nefritis Tubulointerstisialis
I = Sistitis
J = Infeksi Saluran Kemih
Mass Function
Sedangkan mass
function (m) dalam teori Dempster-Shafer adalah tingkat
kepercayaan dari suatu evidence measure sehingga dinotasikan dengan (m).
Untuk mengatasi sejumlah evidence pada teori Dempster-Shafer menggunakan
aturan yang lebih dikenal dengan Dempster’s Rule of Combination.
Dengan :
m1 (X) adalah mass function dari evidence X
m2 (Y) adalah mass function dari evidence Y
m3(Z) adalah mass function dari evidence Z
κ adalah jumlah conflict evidence
m1 (X) adalah mass function dari evidence X
m2 (Y) adalah mass function dari evidence Y
m3(Z) adalah mass function dari evidence Z
κ adalah jumlah conflict evidence
Daftar Pustaka
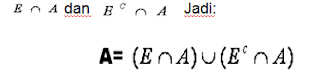






Komentar
Posting Komentar