Inferensi dalam Logika Order Pertama
NAMA
: Dewi Laras
Wijayanti
NPM
: 12114876
KELAS
: 3KA10
MATA KULIAH
: Peng.Teknologi Sistem Cerdas
9.1 Mengubah Inferensi Order Pertama
Menjadi Proporsi
(First
Order Predicate Logic)
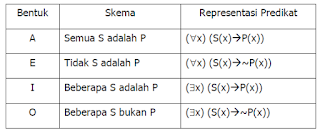
• Representasi 4 kategori silogisme
menggunakan
logika predikat
Kaidah Universal Instatiation merupakan
state
dasar, dimana suatu individual dapat
digantikan
(disubsitusi) ke dalam sifat universal.
• Contoh :
Misal, φ merupakan fungsi proposisi :
(∀ x)
φ(x)
∴
φ(a)
merupakan bentuk yang valid, dimana a
menunjukkan
spesifik individual, sedangkan x adalah
suatu variabel
yang berada dalam jangkauan semua
individu (universal)
• Contoh lain : (∀
x) H(x)
∴
H(Socrates)
• Berikut ini adalah contoh pembuktian
formal silogisme
All men are mortal
Socrates is a man
Therefore, Socrates is mortal
Misal : H = man, M = mortal, s =
Socrates
1. (∀ x)
(H (x) -> M(x))
2. H(s) /
∴
M(s)
3. H(s) ->
M(s) 1 Universal
Instatiation
4. M(s) 2,3
Modus Ponens
9.2
Unifikasi
Unifikasi adalah usaha untuk mencoba membuat
dua ekspresi menjadi identik (mempersatukan keduanya) dengan mencari
substitusi-substitusi tertentu untuk mengikuti peubah-peubah dalam ekspresi
mereka tersebut. Unifikasi merupakan suatu prosedur sistematik untuk memperoleh
peubah-peubah instan dalam wffs. Ketika nilai kebenaran predikat adalah
sebuah fungsi dari nilai-nilai yang diasumsikan dengan argumen mereka,
keinstanan terkontrol dari nilai-nilai selanjutnya yang menyediakan cara memvalidasi
nilai-nilai kebenaran pernyataan yang berisi predikat. Unifikasi merupakan
dasar atas kebanyakan strategi inferensi dalam Kecerdasan Buatan. Sedangkan
dasar dari unifikasi adalah substitusi.
Suatu
substitusi (substitution) adalah suatu himpunan penetapan istilah-istilah
kepada peubah, tanpa ada peubah yang ditetapkan lebih dari satu istilah.
Sebagai pengetahuan jantung dari eksekusi Prolog, adalah mekanisme unifikasi.
Aturan-aturan
unifikasi :
1. Dua
atom (konstanta atau peubah) adalah identik.
2. Dua
daftar identik, atau ekspresi dikonversi ke dalam satu buah daftar.
3. Sebuah
konstanta dan satu peubah terikat dipersatukan, sehingga peubah menjadi terikat
kepada konstanta.
4. Sebuah
peubah tak terikat dipersatukan dengan sebuah peubah terikat.
5. Sebuah
peubah terikat dipersatukan dengan sebuah konstanta jika pengikatan pada peubah
terikat dengan konstanta tidak ada konflik.
6. Dua
peubah tidak terikat disatukan. Jika peubah yang satu lainnya menjadi terikat
dalam upa-urutan langkah unifikasi, yang lainnya juga menjadi terikat ke atom
yang sama (peubah atau konstanta).
7. Dua
peubah terikat disatukan jika keduanya terikat (mungkin melalui pengikatan
tengah) ke atom yang sama (peubah atau konstanta).
9.3 Generalized Modus Ponens (GMP)
Dalam logika Boolean, dengan
aturan `` JIKA X adalah A THEN Y adalah B '',
proposisi X adalah A harus diamati untuk mempertimbangkan
proposisi Yadalah B.
Dalam logika fuzzy, proposisi
`` X adalah A' '',
Dekat dengan premis `` X adalah A '' dapat diamati untuk
memberikan kesimpulan `` Y adalah B' ''
Dekat dengan kesimpulan `` Y adalah B '' .
Sebuah inferensi fuzzy sederhana dapat
direpresentasikan sebagai:
Aturan
|
: JIKA
|
X adalah A THEN
|
Y adalah B
|
|
Fakta
|
:
|
X adalah A'
|
||
Kesimpulan
|
:
|
Y adalah B'
|
Untuk menyimpulkan seperti inferensi
fuzzy kita menggunakan mekanisme yang disebut umum modus ponens. Di
sini, kita menggunakan salah satu berdasarkan implikasi fuzzy Brouwer-Gödel
diungkapkan oleh:
Catatan: Asumsikan -> operator
implikasi Brouwer-Gödel dan o operator
kombinasi, rumus dapat dinyatakan dengan B' = A'o(A-->B) yang
kita gunakan sekarang untuk menyederhanakan notasi.
9.4
Rangkaian Forward Chaining dan Backward Chaining
• Chain (rantai) : perkalian inferensi
yang
menghubung-kan suatu permasalahan dengan
solusinya.
• Forward chaining :
– Suatu rantai yang dicari atau
dilewati/dilintasi dari
suatu permasalahn untuk memperoleh
solusi.
– Penalaran dari fakta menuju konklusi
yang terdapat
dari fakta.
• Backward chaining :
– Suatu rantai yang dilintasi dari suatu
hipotesa tersebut.
– Tujuan yang dapat dipenuhi dengan
pemenuhan
sub tujuannya.
• Contoh rantai inferensi :
gajah(x) -> mamalia (x)
mamalia(x) -> binatang(x)
Karakteristik Forward dan Backward chaining
Forward Chaining
Backward Chaining
Daftar Pustaka






Komentar
Posting Komentar